3Max Planck Institute for Informatics, Saarbrücken
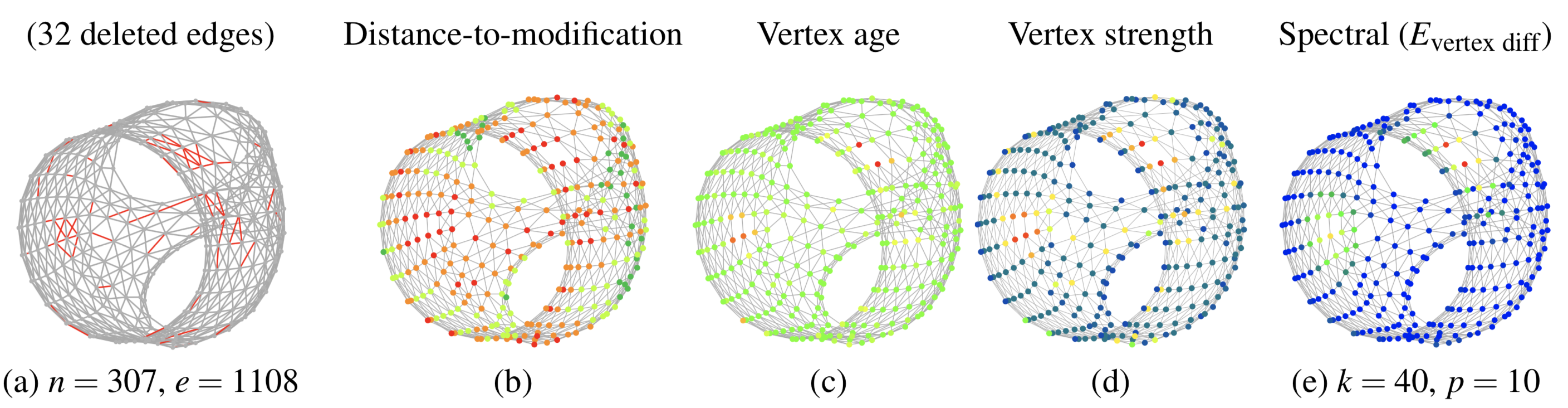

We propose a novel framework for detecting, quantifying and visualizing changes between two snapshots of a dynamic network. Unlike existing approaches, which can be sensitive to minor and isolated changes, and are often based on heuristics, we show how a theoretically justified, inherently multi-scale notion of change, or distortion, can be defined and computed using spectral graph-theoretic tools. Our primary observation is that informative, robust and multi-scale measures of change can be obtained by computing a real-valued function (which we call the distortion function) on the nodes of the input graph, via the optimization of a pre-defined distortion energy in a provably optimal way. Based on extensive tests on a wide variety of networks, we demonstrate the ability of our approach to highlight the evolution of the network in an informative and multi-scale manner.
The Author(s). This is the author's version of the work. It is posted here by permission of the Complex Networks association for your personal use. Not for redistribution. The definitive version is available at link.springer.com.
Imprint
/ Data Protection