Fourier Analysis of
Correlated Monte Carlo Importance Sampling

Gurprit Singh1,4, Kartic Subr2, David Coeurjolly3, Victor Ostromoukhov3, Wojciech Jarosz4
1Max Planck Institute for Informatics, Saarbrücken, 2University of Edinburgh, UK,
3LIRIS/Universite de Lyon 1, France, 4Dartmouth College, USA
In Computer Graphics Forum (Volume 38 issue 1)
Snow
The convergence rate (shown in log-log scale) of Monte Carlo integration with correlated (jittered) samples depends on the importance function (light vs. BSDF). We analyze two Pixels P & Q directly illuminated by a square area light source in (a). Pixel P is fully visible from the light source, which results in a smooth integrand when performing light source surface area sampling (visualized in bottom-left b) and a better convergence rate (c: dot-dashed green curve). C0 discontinuities in the integrand result in bad convergence, which can happen: when using homogenization or Cranley-Patterson rotation (CPr, solid green curve) since it introduces boundary discontinuities; when the light source is partially occluded (Pixel Q); or when sampling the BSDF (in magenta) since this treats the boundary of the light as a C0 discontinuity even when the light is fully visible (visualized in the second column of b).

Abstract

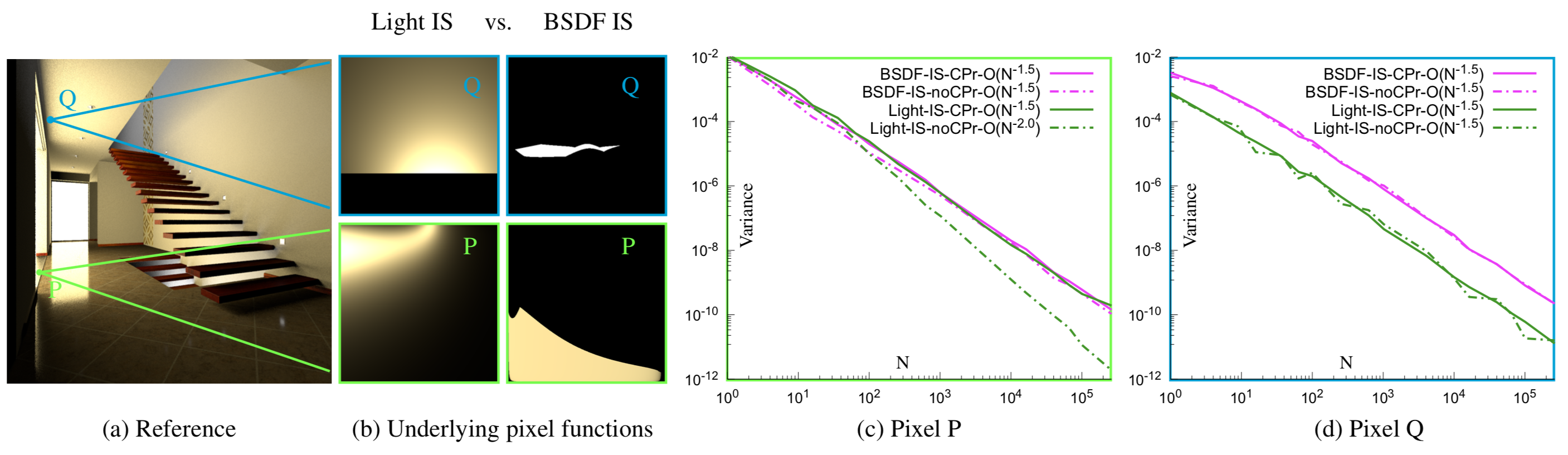
Fourier analysis is gaining popularity in image synthesis as a tool for the analysis of error in Monte Carlo (MC) integration. Still, existing tools are only able to analyze convergence under simplifying assumptions (such as randomized shifts) which are not applied in practice during rendering. We reformulate the expressions for bias and variance of sampling-based integrators to unify non-uniform sample distributions (importance sampling) as well as correlations between samples while respecting finite sampling domains. Our unified formulation hints at fundamental limitations of Fourier-based tools in performing variance analysis for MC integration. At the same time, it reveals that, when combined with correlated sampling, importance sampling (IS) can impact convergence rate by introducing or inhibiting discontinuities in the integrand. We demonstrate that the convergence of multiple importance sampling (MIS) is determined by the strategy which converges slowest and propose several simple approaches to overcome this limitation. We show that smoothing light boundaries (as commonly done in production to reduce variance) can improve (M)IS convergence (at a cost of introducing a small amount of bias) since it removes C0 discontinuities within the integration domain. We also propose practical integrand- and sample-mirroring approaches which cancel the impact of boundary discontinuities on the convergence rate of estimators.

Material

Paper (preprint)
Supplemental document (includes mathematical derivations and analytic evaluations)
Presentation slides: Keynote PDF

Acknowledgements

We are grateful to all the anonymous reviewers for their constructive remarks, Tobias Ritschel for suggesting edits in Figure 7. This work was partially supported by the Fraunhofer and Max Planck cooperation program within the German pact for research and innovation (PFI) and NSF grant CNS-1205521. Kartic Subr was supported by a Royal Society University Research Fellowship and Wojciech Jarosz was partially supported by NSF grant ISS-181279.

Copyright Disclaimer

The Author(s). This is the author's version of the work. It is posted here by permission of The Eurographics Association for your personal use. Not for redistribution. The definitive version is available at diglib.eg.org.

Imprint / Data Protection