Dartmouth College, NH, USA
In ACM Transactions on Graphics (Proceedings of SIGGRAPH) 2017
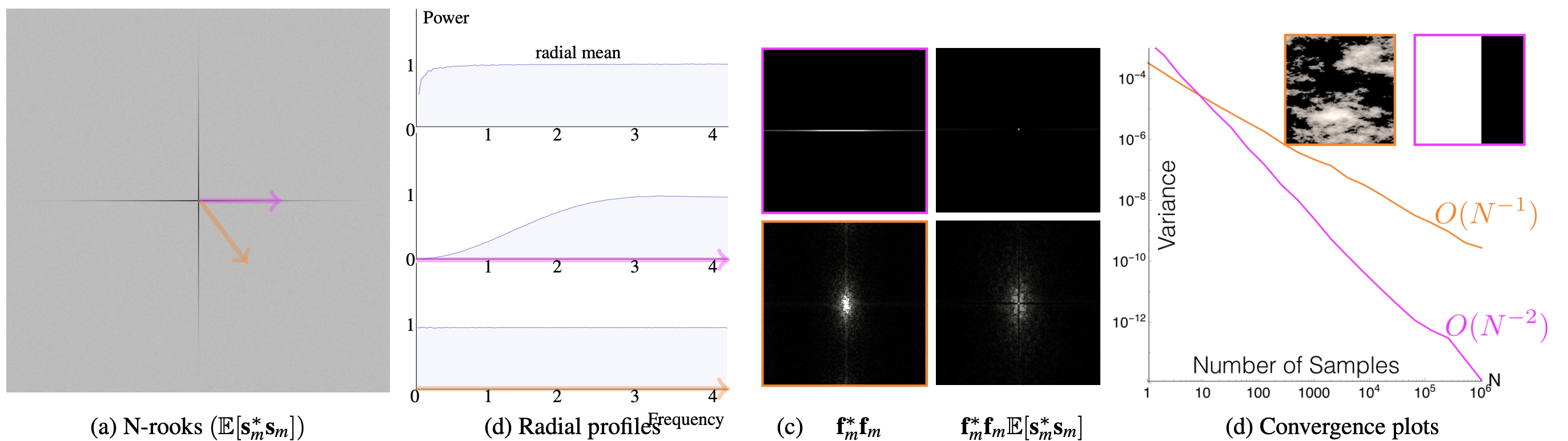
Traditional Monte Carlo (MC) integration methods use point samples to numerically approximate the underlying integral. This approximation introduces variance in the integrated result, and this error can depend critically on the sampling patterns used during integration. Most of the well-known samplers used for MC integration in graphics—--e.g. jittered, Latin-hypercube (N -rooks), multijittered---are anisotropic in nature. However, there are currently no tools available to analyze the impact of such anisotropic samplers on the variance convergence behavior of Monte Carlo integration. In this work, we develop a Fourier-domain mathematical tool to analyze the variance, and subsequently the convergence rate, of Monte Carlo integration using any arbitrary (anisotropic) sampling power spectrum. We also validate and leverage our theoretical analysis, demonstrating that judicious alignment of anisotropic sampling and integrand spectra can improve variance and convergence rates in MC rendering, and that similar improvements can apply to (anisotropic) deterministic samplers.
We would like to thank the anonymous reviewers, whose feedback dramatically improved the final version of this paper, and Emilio Cobanera and Raghu Mahajan for discussions regarding sphere discretization. This work was partially supported by NSF grant CNS-1205521 and a generous gift from Activision
The Author(s) / ACM. This is the author's version of the work. It is posted here for your personal use. Not for redistribution. The definitive Version of Record is available at doi.acm.org.
Imprint
/ Data Protection