Gurprit Singh

Corentin Salaun¹, Adrien Gruson^2,3, Binh-Son Hua⁴, Toshiya Hachisuka⁵, Gurprit Singh¹

¹Max Planck Institute for Informatics, Saarbrücken ² McGill University, Canada ³ Ècole Supèrieure de Technologie (ÈTS), Canada ⁴ VinAI Research, Vietnam ⁵ University of Waterloo, Canada

SIGGRAPH 2022 / ACM Transactions on Graphics, Volume 41 issue 4, July 2022

Given an integrand (a), we first sample (b) f(x) as in Monte Carlo (MC) integration. (c-d) Traditional MC estimator can be interpreted as fitting a constant model function to the sample values, with the integral of this constant function equals to F. (e) We, instead, propose to use a non-constant model function such as a polynomial, which is then fitted to the sampled values. (f) The resulting estimator is based on control variates; we add the analytical integral of the model function to MC integration of the difference between the original integrand and the model function.

Abstract

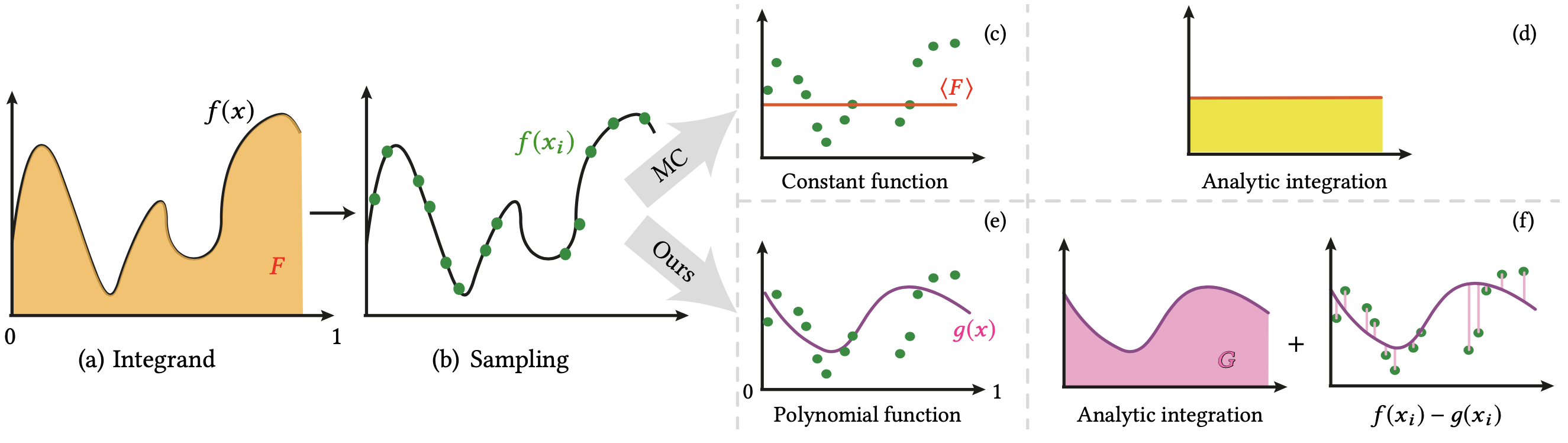
Monte Carlo integration is typically interpreted as an estimator of the expected value using stochastic samples. There exists an alternative interpretation in calculus where Monte Carlo integration can be seen as estimating a constant function---from the stochastic evaluations of the integrand---that integrates to the original integral. The integral mean value theorem states that this constant function should be the mean (or expectation) of the integrand. Since both interpretations result in the same estimator, little attention has been devoted to the calculus-oriented interpretation. We show that the calculus-oriented interpretation actually implies the possibility of using a more complex function than a constant one to construct a more efficient estimator for Monte Carlo integration. We build a new estimator based on this interpretation and relate our estimator to control variates with least-squares regression on the stochastic samples of the integrand. Unlike prior work, our resulting estimator is provably better than or equal to the conventional Monte Carlo estimator. To demonstrate the strength of our approach, we introduce a practical estimator that can act as a simple drop-in replacement for conventional Monte Carlo integration. We experimentally validate our framework on various light transport integrals.

Acknowledgements

We thank the anonymous reviewers for their comments that helped shape the paper. We thank the following for scenes used in our experiments: Wing42 (Dinning-room), nacimus (Bathroom), Karl Li (PBRT-book), julioras3d (chopper- titan), Greyscalegorilla (vw-van), Benedikt Bitterli (Teapot), MtChimp2313 (House). This project is supported in part by the Natural Sciences and Engineering Research Council of Canada (NSERC) RGPIN1507.

Regression-based Monte Carlo Integration

Abstract

Material

Acknowledgements

Copyright Disclaimer