Joint Sampling and Optimisation for Inverse Rendering
Martin Balint, Karol Myszkowski, Hans-Peter Seidel, Gurprit Singh
Max Planck Institute for Informatics, Saarbrücken, Germany
SIGGRAPH Asia 2023
We simultaneously optimise the spiral’s base colour, metalness and roughness. Our gradient meta-estimator quickly recovers the gradient with just one finite-difference and two proportional samples per pixel. Adam’s default first moment estimator cannot adapt as quickly and often overshoots. After tuning Adam’s hyperparameters for this specific problem, it approaches our method at 32 spp and matches it only at 64 spp.
Abstract
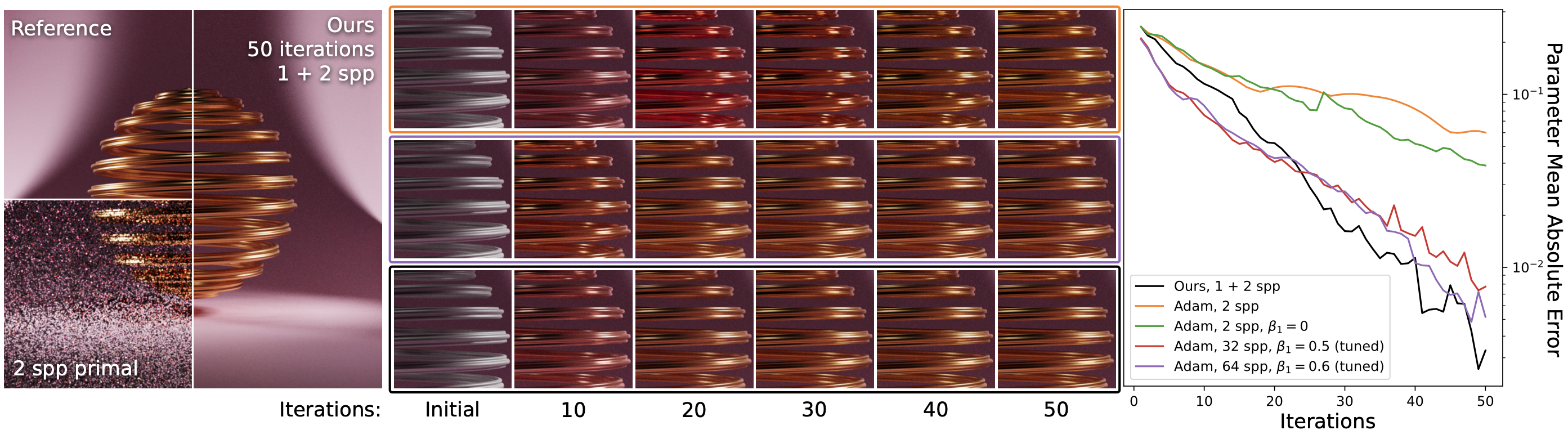
When dealing with difficult inverse problems such as inverse rendering, using Monte Carlo estimated gradients to optimise parameters can slow down convergence due to variance. Averaging many gradient samples in each iteration reduces this variance trivially. However, for problems that require thousands of optimisation iterations, the computational cost of this approach rises quickly.
We derive a theoretical framework for interleaving sampling and optimisation. We update and reuse past samples with low-variance finite-difference estimators that describe the change in the estimated gradients between each iteration. By combining proportional and finite-difference samples, we continuously reduce the variance of our novel gradient meta-estimators throughout the optimisation process. We investigate how our estimator interlinks with Adam and derive a stable combination.
We implement our method for inverse path tracing and demonstrate how our estimator speeds up convergence on difficult optimisation tasks.
Acknowledgements
This work is supported by an academic gift from Meta. We thank the anonymous reviewers for their valuable feedback.
Copyright Disclaimer
The Author(s) / ACM. This is the author's version of the work. It is posted here for your personal use. Not for redistribution. The definitive Version of Record is available at doi.acm.org.
Imprint
/ Data Protection
